o MARGARITA DE
JESÚS CARVAJAL.
o MARTHA EDITH
CASTAÑO A.
o ROSA MARIA
RAMIREZ G.
o GRUPO 06
ANSERMA CALDAS
martes, 22 de septiembre de 2015
Se
conoce como matemática o matemáticas, según corresponda a la costumbre, al
estudio de todas aquellas propiedades y relaciones que involucran a los entes
abstractos, como ser los números y figuras geométricas, a través de notaciones
básicas exactas y del razonamiento lógico.
ALGUNOS EJEMPLOS MATEMATICOS
Ejemplo de
Polinomios
A diferencia de
la Aritmética que siempre expresa cantidades concretas utilizando sólo números,
el álgebra expresa las cantidades usando números y letras, y una misma cantidad
puede expresar cantidades conocidas o desconocidas.
A la expresión
de una cantidad con números y letras se le llama término. Lo más común es usar
las letras minúsculas.
Un término
algebraico puede estar formado por números, por letras o por combinaciones de
números y letras. Los términos formados sólo por números, expresan cantidades
concretas. Los términos formados por letras o por números y letras pueden
expresar cualquier cantidad conocida o desconocida.
Los polinomios
representan un solo número, pero están formados por dos o más términos, unidos
mediante signos de suma o resta. Cuando tiene dos términos, se les llama
binomios; si tienen tres términos, trinomios. Cuando tienen cuatro o más
términos se les llama solamente polinomios. Cada uno de sus términos Puede
tener signo positivo o negativo o ser fraccionarios.
(Para no
confundir con el término x, usaremos el asterisco (*) para indicar una
multiplicación).
Los términos
literales están formados por coeficientes. El coeficiente numérico indica
cuántas veces se suma el coeficiente literal. Así por ejemplo, 3x dice que x se
sumará 3 veces: x+x+x o bien, que se el número que representa la letra x se
multiplica por 3 (3*x).
Algunos términos
sólo contienen coeficientes literales. Por ejemplo ac. Estos indica que la c se
sumará a veces (c+c+c+c+c+c… a veces) o que a se sumará c veces (a+a+a+a+a… c
veces) lo más sencillo es entender que se multiplican. Así, ac es la
multiplicación de a por c (a*c).
Cuando un
término consta de un coeficiente literal, se considera que su coeficiente es 1.
Por ejemplo y es igual a 1 por y (1*y).
Otra
característica de los términos es el grado. El grado de un término está
determinado por el exponente de la expresión. El grado puede ser absoluto o en
relación a una letra.
Por ejemplo, en
el término 4ab, el grado absoluto es 1, ya que no está expresada ninguna otra
potencia. En la expresión 4a3b5 el grado absoluto se calcula sumando los
exponentes. En este caso el grado absoluto es 8.
El grado en
relación a una letra, indica el grado de un término en relación al exponente de
una de las letras que lo integran. En el término ab2c4, es un término de primer
grado en relación a la letra a; es de segundo grado en relación a la letra b y
es de cuarto grado en relación a la letra c.
En algunas
ocasiones se puede usar un exponente literal: abm, donde se indica que b se
elevará a la m potencia.
Es común
organizar un polinomio en relación al grado de cada término en relación a una
letra. Por ejemplo en el polinomio ab2 + 3ab – 2a2 – ab + b2, si lo
ordenamos en relación al valor de a, lo escribiremos así: – 2a2 + 3ab – ab
+ ab2 + b2. Si lo ordenamos según el grado de b, lo escribiremos
así: b2+ ab2+ 3ab – ab – 2a2.
En un polinomio,
los términos que tienen los mismos grados en los coeficientes literales, pero
diferentes coeficientes numéricos, se suman para simplificar el polinomio. En
el siguiente ejemplo, b2+ ab2+ 3ab – ab – 2a2, 3ab y –ab, tienen los mismos
coeficientes numéricos y en el mismo grado, por lo que se suman para
simplificarlos. En este caso, el polinomio quedará así: b2+ ab2+ 2ab – 2a2.
Los términos
fraccionarios, al igual que las fracciones aritméticas, están formados por dos
números y representan la fracción de un todo mediante una división. Así, un
término como el siguiente: 3ab2/6cd4 + 2a2b/3cd es un binomio, ya que
consta de dos términos fraccionarios.
36 ejemplos de
polinomios
A + b
a2 + b
a + b2
a2b2 + ab
abc + bc
a2b + c
a + b2c
abc2 + abc
a2 - b2 +
c2
a+ b2 – x –
y
2a + 3b + 5c – 7
4ab - 4
3x + 2x2 –
4x3 – 5x4
4y – 6a
ab2/ax – a2b/ax2
- x4/y2 + x3/y
ab/bc + bc/ac
xy + yz
xyz - z
16ab + 2a3b2
5yz – 5y – z
6cz - c
4a2 + 2ab +
b2
4ab5 - 1
b3 + c4
ax3/b2y – a2x/b3y
a2x/b3y – ax3/b2y
m2n3 + o2n3
a2mn + b2nm
m2n/op3 +
4np2
6c3d + abc + a2bc4
a4x3/b5y2 –
ab3/x3y3
abcd + ab + bc +
cd + ad
ab/cd + cd/ab
cd/ab + ab/cd -
3a2b/4c3d
ab2c3d + ab3c3d
- ab2c2d
Ejemplo de
Monomios
A diferencia de
la Aritmética que siempre expresa cantidades concretas utilizando sólo números,
el álgebra expresa las cantidades usando números y letras, y una misma cantidad
puede expresar cantidades conocidas o desconocidas.
A la expresión
de una cantidad con números y letras se le llama término. Lo más común es usar
las letras minúsculas.
Un término
algebraico puede estar formado por números, por letras o por combinaciones de
números y letras. Los términos formados sólo por números, expresan cantidades
concretas. Los términos formados por letras o por números y letras pueden
expresar cualquier cantidad conocida o desconocida.
Los monomios
son representaciones numéricas formadas por un solo término. Pueden tener signo
positivo o negativo o ser fraccionarios. Cuando son de signo positivo, el signo
no se escribe. Cuando son negativos, van precedidos del signo menos (-)
(Para no
confundir con el término x, usaremos el asterisco (*) para indicar una
multiplicación).
Los términos
literales están formados por coeficientes. El coeficiente numérico indica
cuántas veces se suma el coeficiente literal. Así por ejemplo, 4x dice que x se
sumará 4 veces: x+x+x+x o bien, que se el número que representa la letra x se
multiplica por 4 (4*x).
Algunos términos
sólo contienen coeficientes literales. Por ejemplo ac. Estos indican que la c
se sumará a veces (c+c+c+c+c+c… a veces) o que a se sumará c veces (a+a+a+a+a…
c veces) lo más sencillo es entender que se multiplican. Así, ac es la
multiplicación de a por c (a*c).
Cuando un
término consta de un coeficiente literal, se considera que su coeficiente es 1.
Por ejemplo y es igual a 1 por y (1*y).
Otra
característica de los términos es el grado. El grado de un término está
determinado por el exponente de la expresión. El grado puede ser absoluto o en
relación a una letra.
Por ejemplo, en
el término 4ab, el grado absoluto es 1, ya que no está expresada ninguna otra
potencia. En la expresión 4a3b5 el grado absoluto se calcula sumando los
exponentes. En este caso el grado absoluto es 8.
El grado en relación
a una letra, indica el grado de un término en relación al exponente de una de
las letras que lo integran. En el término ab2c4, es un término de primer grado
en relación a la letra a; es de segundo grado en relación a la letra b y es de
cuarto grado en relación a la letra c.
En algunas
ocasiones se puede usar un exponente literal: abm, donde se indica que b se
elevará a la m potencia.
Los términos
fraccionarios, al igual que las fracciones aritméticas, están formados por dos
números y representan la fracción de un todo mediante una división. Así, un
término como el siguiente: 3ab2/6cd4 es un monomio, ya que constan de solo
término, que en este caso es fraccionario.
36 ejemplos de
monomios:
ab
a2b
-ab2
a2b2
abc
-a2bc
ab2c
-abc2
-a2b2c2
ab2xy
2a
4ab
-3x
-4y
ab2/ax
x4/y2
ab/bc
xy
xyz
16ab
-5yz
6cz
2a2
-4ab5
b3c4
-ax3/b2y
a2x/b3y
-m2n3o2
a2mn
-m2n/op3
-6c3d
a4x3/b5y2
abcd
ab/cd
cd/ab
ab2c3d
Ejemplo de Ley
de los signos
La ley de
los signos es una ley que corresponde y atiende a los números positivos y
negativos de los números enteros.
Esta ley se
ocupa del sentido de los números y ocupa los signos “+” y “-”, siendo el signo
+ nombrado “más” y correspondiendo a los números positivos y el signo – de
nombre “menos” corresponde al negativo y es de los negativos.
En relación a la
suma y la resta de números enteros el resultado será positivo en el caso del
signo + y negativo en el caso del signo -.
Pero en el caso
de la multiplicación y la división, sólo se presenta el positivo si ambos
números son positivos y negativo si alguno es positivo y su contrario negativo,
lo mismo sucede en las ecuaciones algebraicas.
Ejemplos de
operaciones con ley de los signos:
1.- Suma:
Se suman con
el mismo signo:
(-4) + (-5) =
-8
(+3) + (+5) = +8 = 3+5 = 8
En el caso de
distinto signo se restan y se coloca el signo que tiene mayor valor absoluto,
como si siguiéramos la recta numérica.
(-4) + 5 = 1
4 + (-5) = -1
Aquí se
coloca en el resultado el único signo que existe en el número.
2.- Resta:
El principio
es técnicamente igual que en la suma, poniéndose el sentido del signo marcado
cuando son iguales:
(+8) - (+5) =
+3
(-9) - (-4) = -5
En los
siguientes casos se aplica el sentido de la recta numérica tal como sucede en
la suma:
(-4) - (+2) =
-2
(+4)-(-2)= +2
3.-
Multiplicación:
En la
multiplicación, cuando se realiza la operación con números de signo igual, el
resultado es positivo, no importa si el signo es + o –
(+5) x (+4) =
+20
(-5) x (-4) = +20
Pero en el
caso de que los signos sean diferentes el resultado será negativo sin importar
el signo de que se trate:
(-3) x (+5) =
-15
(-6) x (+3) = 18
4.- División:
En la
división cuando se dividen números de igual signo el resultado es positivo,
independientemente del signo de que se trate:
(+9) ÷ (+4) =
+2.25
(-8) (-2) = +4
Y en el caso
de signos distintos el resultado será negativo, independientemente del signo de
que se trate:
(-9) ÷ +2 =
-7
(+9) ÷ (-2) = -7
Ejemplo de
Ley de los signos
La ley
de los signos es una ley que corresponde y atiende a los números positivos
y negativos de los números enteros.
Esta ley se
ocupa del sentido de los números y ocupa los signos “+” y “-”, siendo el signo
+ nombrado “más” y correspondiendo a los números positivos y el signo – de
nombre “menos” corresponde al negativo y es de los negativos.
En relación a
la suma y la resta de números enteros el resultado será positivo en el caso del
signo + y negativo en el caso del signo -.
Pero en el
caso de la multiplicación y la división, sólo se presenta el positivo si ambos
números son positivos y negativo si alguno es positivo y su contrario negativo,
lo mismo sucede en las ecuaciones algebraicas.
Ejemplos de
operaciones con ley de los signos:
1.- Suma:
Se suman con
el mismo signo:
(-4) + (-5) =
-8
(+3) + (+5) = +8 = 3+5 = 8
En el caso de
distinto signo se restan y se coloca el signo que tiene mayor valor absoluto,
como si siguiéramos la recta numérica.
(-4) + 5 = 1
4 + (-5) = -1
Aquí se
coloca en el resultado el único signo que existe en el número.
2.- Resta:
El principio
es técnicamente igual que en la suma, poniéndose el sentido del signo marcado
cuando son iguales:
(+8) - (+5) =
+3
(-9) - (-4) = -5
En los
siguientes casos se aplica el sentido de la recta numérica tal como sucede en
la suma:
(-4) - (+2) =
-2
(+4)-(-2)= +2
3.-
Multiplicación:
En la
multiplicación, cuando se realiza la operación con números de signo igual, el
resultado es positivo, no importa si el signo es + o –
(+5) x (+4) =
+20
(-5) x (-4) = +20
Pero en el
caso de que los signos sean diferentes el resultado será negativo sin importar
el signo de que se trate:
(-3) x (+5) =
-15
(-6) x (+3) = 18
4.- División:
En la
división cuando se dividen números de igual signo el resultado es positivo,
independientemente del signo de que se trate:
(+9) ÷ (+4) =
+2.25
(-8) (-2) = +4
Y en el caso
de signos distintos el resultado será negativo, independientemente del signo de
que se trate:
(-9) ÷ +2 =
-7
(+9) ÷ (-2) = -7
Ejemplo de
Álgebra
Se
llama álgebra a la ciencia que se ocupa de expresar en la forma más
general y universal posible las operaciones de los números y matemáticas
aplicadas.
Aritmética
Física
Geometría
Matemáticas
Química
Trigonometría
El álgebra
estudia la estructura de las matemáticas aplicadas en la forma más abstracta
posible, explicándola mediante fórmulas y operaciones. Esto permite que existan
fórmulas que sirven como parámetro para realizar las operaciones.
Para lograr
esto el álgebra se sirve de signos de operación tales como:
Suma +
Resta -
Multiplicación
x o (.)
División ÷ o
(:)
Y se sirve
de fórmulas:
bxh2 (base
por altura sobre dos)
Donde se
expresa la base por la altura al cuadrado
Históricamente el
álgebra se remonta a los babilonios, quienes lograron realizar trabajos
matemáticos equiparables a las ecuaciones de 1º y 2º grado, posteriormente se
vio influenciada por los números arábigos, siendo invadido a lo largo de la
historia por influencia de muchas culturas culminando finalmente en una serie
de signos matemáticos y símbolos que son los parámetros del algebra.
Signos
algebraicos:
Estos son
todos los signos y símbolos usados en algebra y matemáticas,
mediante su combinación se pueden formular operaciones algebraicas y formulas
algebraicas, se representan los números mediante letras:
Ejemplos de
álgebra en aritmética:
En aritmética
existen aplicaciones equivalentes en el álgebra y se aplica a las operaciones
fundamentales:
1.-Suma
algebraica
Sumando a y b = a+b
(a+b) +c =
a+b+c
Suma de
números algebraicos: (+2) + (+3) = (+5)
2.- Resta
algebraica
a-b = a-b
c-b-a = -cba
-4 -6 = -9
Resta de
números algebraicos: (+8) - (+5) = -8-5=3
3.- División
algebraica
División de
números algebraicos: (+18) : (+3) = +6
Esta división
también se puede realizar mediante quebrados
8a2
2a
4.- Multiplicación
algebraica. En esta multiplicación existe la propiedad conmutativa
y no siempre dan el resultado de sumar, también pueden reducir al tener
la ley de los signos.
Bn · Bm =
bn+m
Multiplicación
de 3a2 por 4a3
3a2 X 4a3
= 3aX4a3+4 = 12a5
Ejemplos de
álgebra en física:
Teoría de la
relatividad de Einstein
E = mc2
Ejemplos de
álgebra en geometría:
Área de un
cuadrado A = bxh2
Área de un circulo A=πr2
Ejemplos de
álgebra en química:
Ecuación
química del agua
H2+O2
Ejemplos de
álgebra en trigonometría:
2tg x –
3 oct x – 1 = 0
Mas ejemplos de Matemáticas:
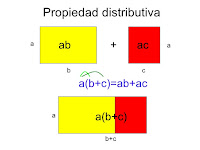
Razón matemática y ejemplos
1. RAZÓN MATEMÁTICA
2. Una razón
matemática es el cociente entre dos medidas de diferentes magnitudes.
Generalmente, se expresa como «a es a b». En una razón al primer término se le
llama antecedente y al segundo se llama consecuente. a Antecedente b
Consecuente
3. La razón se puede
escribir de diferentes maneras. Por ejemplo la razón entre 3 y 2 se puede
escribir: 3:2 ó 3 Y se lee 3 es a 2 ó 3 a 2 2
4. Una razón también
se puede expresar como el cociente (resultado de la división) entre el
antecedente y el consecuente. 3 dividido 2 es igual a 1,5; es decir, la razón
entre 3 y 2 es 1,5.
5. Si en la razón el
antecedente y el consecuente comparten la misma unidad se puede expresar como
un cociente adimensional. Si por el contrario son de diferentes dimensiones en
la razón se escriben de manera explícita; por ejemplo la razón entre una
distancia recorrida de 8 km en una hora; se expresa como 8 km / h 5
6. VEAMOS ALGUNOS EJEMPLOS
DE RAZÓN EJEMPLO 1: Como la razón es el cociente entre dos magnitudes,
supongamos que: La primera Magnitud es la distancia recorrida por un automóvil.
La segunda Magnitud es el tiempo que gasta el automóvil en recorrer cierta
distancia. Entonces la razón que tendríamos es: distancia recorrida tiempo
empleado Supongamos que un automóvil recorrió 130 kilómetro, en un tiempo de 2
horas; la razón es: 130Km 2 horas
7. EJEMPLO 2: María
quiere preparar un torta Irlandesa, utiliza 500 gramos de harina (lista para
torta), 180 gramos de margarina, 240 gramos de huevos, 150 ml de agua. Para
comparar las cantidades que se van a emplear , se utilizan razones matemáticas.
Por ejemplo la razón entre la cantidad de harina utilizada y la margarina es:
500 gramos de harina 180 gramos de margarina Se lee 500 gramos de harina es a
180 gramos de margarina ó 500 es a 180.
8. EJEMPLO 3: En una
fiesta hay 3 hombres por cada 5 mujeres la razón por medio de la cual se puede
expresar esta situación es: 3:5 ó 3 5 Cualquiera de las dos expresiones se
puede leer como: « 3 es a 5 » ó « 3 a 5 »
TRABAJO
DE
MATEMATICAS
1-. PRODUCTO CARTESIANO
El producto cartesiano de dos conjuntos A x B
es el conjunto de todos los pares ordenados que se pueden formar con un
elemento perteneciente al conjunto A y un elemento del conjunto B.
Los elementos de A x B son pares ordenados.
Cada par que se forma con un elemento del conjunto A y uno del conjunto B, en
ese orden y recibe el nombre de par ordenado. Sus elementos se colocan
entre paréntesis, separados por coma.
ejemplo n° 1:
ejemplo n° 2:
Si A ={1,2} y B ={-1,O,1} entonces A x B ={(1,-1),
(1,0), (1,1), (2,-1), (2,0), (2,1)}. A tiene 2 elementos, B tiene
3, y A x B tiene 2 x 3 = 6
Ejemplo n° 3:
Si A = B = R, entonces R al
cuadrado es llamado el plano cartesiano. Las caricaturas y demás
objetos bidimensionales viven en R al cuadrado: un círculo no es otra cosa
que cierto subconjunto de R al cuadrado (dé un ejemplo). Nosotros,
los seres tridimensionales, vivimos en R al cuadrado x R
2-. CONJUNTO CARTESIANO
Es la agrupación en un todo de objetos bien
diferenciados en el la mente o en la intuición, por lo tanto, estos objetos son
bien determinados y diferenciados.
Ejemplo n° 1:
Este ejemplo gráfico nos muestra la agrupación llamado Alumnos de
Colegio con sus elementos que serían: Luis, Antonio, Paula y Pánfilo
3-. RELACION MATEMÁTICA
El concepto de relación implica la idea de
correspondencia entre los elementos de dos conjuntos que forman parejas ordenadas.
Cuando se formula una expresión que liga dos
o más objetos entre sí, postulamos una relación (no necesariamente matemática)
Por ejemplo:
Samuel es padre de Irma. (Samuel, Irma)
Del ejemplo anterior podríamos decir
matemáticamente que:
S ---> I
Podemos definir la relación como la
correspondencia que hay entre TODOS o ALGUNOS del primer conjunto con UNO o MÁS
del segundo conjunto.
Ejemplos de relación
A = {1, 4, 6}
B = {2, 3, 7}
La relación que existe entre A y B es mayor
que, por lo que:
ARB={ (6,2) (4,2) (6,3) (4,3)}
4-. TIPOS DE RELACION:
RELACION REFLEJA ( O REFLEXIVA )
R es una relación refleja en un conjunto A no
vacío , si y sólo si cada elemento de
él está relacionado consigo mismo:
a ð A ð a R a
Ejemplo:
A = { 1 , 2 , 3 }
R = { ( 1 , 1 ) , ( 1 , 3 ) , ( 2 , 2 ) , ( 3
, 2 ) , ( 3 , 3 ) }
RELACION SIMETRICA
R es una relación simétrica en un conjunto A
no vacío , si y sólo si cada par de
elementos de él satisface lo siguiente:
a R b ð b R a
Ejemplo:
A = { 1 , 2 , 3 }
R = { ( 1 , 3 ) , ( 2 , 3 ) , ( 3 , 1 ) , ( 3
, 2 ) , ( 3 , 3 ) }
RELACION ANTISIMETRICA
R es una relación antisimétrica en un
conjunto A no vacío , si y sólo si cada par de
elementos de él satisface lo siguiente:
a R b ð b R a ð a = b
Ejemplo:
A = { 1 , 2 , 3 }
R = { ( 1 , 3 ) , ( 2 , 1 ) , ( 2 , 2 ) , ( 3
, 2 ) }
RELACION TRANSITIVA
R es una relación transitiva en un conjunto A
no vacío , si y sólo si cada trío de
elementos de él satisface lo siguiente:
a R b ð b R c ð a R c
Ejemplo:
A = { 1 , 2 , 3 }
R = { ( 1 , 1 ) , ( 1 , 3 ) , ( 2 , 1 ) , ( 2
, 3 ) , ( 3 , 1 ) , ( 3 , 3 ) }
5-. CLASIFICACION DE RELACIONES
RELACION DE EQUIVALENCIA
R es una relación de equivalencia en un
conjunto A no vacío , si y sólo si es
refleja, simétrica y transitiva en ese
conjunto A .
Ejemplo:
La relación "igual que" ( = ) en el
conjunto de los números enteros.
Sean a , b y c números enteros cualesquiera,
entonces:
a = a ( Reflexividad )
a = b ð b = a ( Simetría )
a = b ð b = c ð a = c ( Transitividad )
RELACION DE ORDEN
R es una relación de orden en un conjunto A
no vacío , si y sólo si es refleja,
antisimétrica y transitiva en ese conjunto A
.
Ejemplo:
La relación "menor o igual que" ( ð
) en el conjunto de los números enteros.
Sean a , b y c números enteros cualesquiera,
entonces:
a ð a ( Reflexividad )
a ð b ð b ð a ð a = b ( Antisimetría )
a ð b ð b ð c ð a ð c ( Transitividad )
6-. FUNCION
Sean A y B conjuntos no vacíos, f es una
función de A en B , si y sólo si
f es una relación de A a B que a cada
elemento de A le hace corresponder un y
sólo un elemento de B .
Ejemplo:
A = { a , e , i }
B = { 1 , 3 , 5 , 7 }
f = { ( a , 3 ) , ( e , 7 ) , ( i , 7 ) }
Además su dominio es:
Dom f = A
Su codominio es:
Codom f = B
Su recorrido ( o rango ) es:
Rec f = { 3 , 7 }
Este último es el conjunto de las imágenes de
A bajo f .
7-. FUNCION VALOR-ABSOLUTO
La funcion valor absoluto esta definida de la
siguiente manera:
Graficamente la función IxI es
Si x es positivo no afecta la función en el
número
Si x es negativo la función "lleva al
numero" a su inverso aditivo
El valor absoluto de un número real nunca es
negativo
Al valor absoluto de un número también se le
denomina Módulo
Antes de resolver algunos ejercicios veamos
algunas propiedades básicas del valor absoluto. Es claro que la definición de
valor absoluto que
8-. FUNCION PARTE ENTERA
La función parte entera
está definida por:
1. La función piso si es el menor número de
los dos números enteros entre
los que está comprendido x. De esta forma, si x es un número entero, su parte entera es el mismo
entero. Si x = 5/2 entonces su parte entera será 2.
2. La función techo si es el mayor número de
los dos números enteros entre
los que está comprendido x.
Siempre se tiene que
y a la izquierda hay una igualdad si y sólo
si x es entero.
Para todo entero k y para todo número real x se tiene:
El redondeo usual del número x al
entero más próximo se puede expresar como la parte entera de x + 0,5.
La derivada de la función parte entera no
está definida en los números enteros, y en cualquier otro punto
vale 0.
9-. FUNCION CUADRÁTICA
Decimos que una función es cuadrática si se
puede expresar de la forma
f(x)= ax2+bx+c
donde a,b y c son constantes y a # 0
La gráfica de una fución cuadrática es una
parábola y su dominio es el conjunto de los númeos reales.
Si a>0, se dice que la parábola es
positiva y, en este caso, abre hacia arriba. Si a<0, la parábola es negativa
y abre hacia abajo.
A continuación se muestran dos funciones
cuadráticas con sus respectivas gráficas y una lista de algunas de las parejas
ordenadas que pertenecen a dichas funciones cuadràticas.
f(x)= x2 - 5x + 4 f(x)= - x2 - 5x + 4
x
|
f(x)
|
0
|
4
|
1
|
0
|
2
|
-2
|
4
|
0
|
5
|
4
|
x
|
f(x)
|
-6
|
-2
|
-5
|
4
|
-1
|
8
|
0
|
4
|
1
|
-2
|
10-. FUNCION LOGARITMO
La expresión lnx se lee "logaritmo
natural de x".
La siguiente figura ilustra la interpretación
de lnx como un área, para el caso x > 1:
Grafica de la función logaritmo natural:
Para calcular el valor aproximado de y cuando x =
2, se puede aplicar la Regla de Simpson.
11-. FUNCION Ex (no la encontré)
12-. FUNCION RAIZ CUADRADA
En matemáticas, la raíz cuadrada de un número real no negativo x es el número real no
negativo que, multiplicado con sí mismo, da x. La raíz cuadrada de x se denota por "x.
Por ejemplo, "16 = 4, ya que 4 × 4 = 16, y "2 = 1,41421... . Las raíces
cuadradas son importantes en la resolución de ecuaciones cuadráticas.
La generalización de la función raíz cuadrada
a los números negativos da lugar a los números imaginarios y al campo de los números complejos.
Las siguientes propiedades de la raíz cuadrada son
válidas para todos los números positivos x, y:
para todo número real x
La función raíz cuadrada,
en general, transforma números racionales en números algebraicos; "x es
racional si y sólo si x es
un número racional que puede escribirse como fracción de dos cuadrados perfectos. Si el denominador es 12 =
1, entonces se trata de un número natural. Sin embargo, "2 es irracional.
La función raíz cuadrada transforma la superficie de un cuadrado en la longitud de su lado.
13-. TIPOS DE FUNCIONES :
FUNCION INYECTIVA
Sea f una función de A en B , f es una función
inyectiva , si y sólo si cada
elemento de B es imagen de a lo más un
elemento de A , bajo f .
Ejemplo:
A = { a , e , i }
B = { 1 , 3 , 5 , 7 }
f = { ( a , 7 ) , ( e , 1 ) , ( i , 5 ) }
FUNCION EPIYECTIVA ( O SOBREYECTIVA )
Sea f una función de A en B , f es una
función epiyectiva , si y sólo si cada
elemento de B es imagen de al menos un
elemento de A , bajo f .
Ejemplo:
A = { a , e , i , o , u }
B = { 1 , 3 , 5 , 7 }
f = { ( a , 1 ) , ( e , 7 ) , ( i , 3 ) , ( o
, 5 ) , ( u , 7 ) }
FUNCION BIYECTIVA
Sea f una función de A en B , f es una
función biyectiva , si y sólo si f es
epiyectiva e inyectiva a la vez .
Ejemplo:
A = { a , e , i , o , u }
B = { 1 , 3 , 5 , 7 , 9 }
f = { ( a , 5 ) , ( e , 1 ) , ( i , 9 ) , ( o
, 3 ) , ( u , 7 ) }
Teorema:
Si f es biyectiva , entonces su inversa f - 1
es también una función y además
biyectiva
Suscribirse a:
Entradas (Atom)